Straight Line and a Point

The line $3x+2y=24$ meets the $\mathrm{y}$-axis at $\mathrm{A}$ & the $\mathrm{x}$-axis at $\mathrm{B}$. The perpendicular bisector of $\mathrm{AB}$ meets the line through $(0, -1)$ parallel to $\mathrm{x}$-axis at $\mathrm{C}$. Then the area ( in square units ) of the triangle $\mathrm{ABC}$ is

The equation of the perpendicular bisectors of the sides $AB$ and $AC$ of a  $\Delta ABC$ are  $x-y+5=0$  and  $x+2y=0$  respectively. If the point $A$ is  $\left(1,-2\right),$ then the equation of the line $BC$ is.

Suppose a triangle is formed by $x+y=10$ and the coordinate axes. Then the number of points $\left(x,y\right)$ where $x$ and $y$ are natural numbers, lying inside the triangle is

Look at the graph and answer the question.

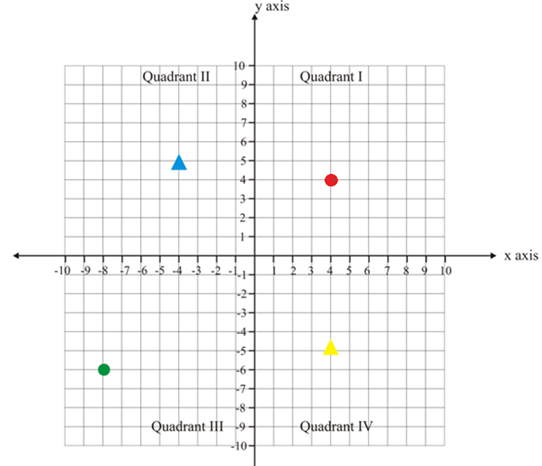
The blue triangle is at point $\left(-4, 5\right)$. What is at $\left(4, -5\right)?$ _____.

The equation of a line though the point $(1,2)$ whose distance from the point $(3,1)$ has the greatest value is

The perpendicular distance from the point $\left(1,2\right)$ to common chord of the circles $2 x+4 y-4=0$ and $x^2+y^2+4x-6y-3=0$ is units.

The number of lines that can be drawn through the point $\left(4, -5\right)$ at a distance of $10$ units from the point $\left(1, 3\right)$ is_______.

If a square $ABCD$ where $A(0,0),B(2,0),C(2,2),D(0,2)$ undergoes the following transformations successively,

$\left(\mathrm{i}\right)$ $f_1(x,y)⟶(y,x)$
$\left(\mathrm{ii}\right)$ $f_2(x,y)⟶(x+3y,y);$

$\left(\mathrm{iii}\right)$ $f_3(x,y)⟶\left(\frac{x-y}{2},\frac{x+y}{2}\right)$

Then the final figure would be a _______.

If $p_1, p_2$ denote the lengths of perpendiculars from $(2, 3)$ onto the lines given by $15{\mathrm{x}}^2+31\mathrm{xy}+14{\mathrm{y}}^2=0$, and if $p_1>p_2,$ then $p_1^2+\frac{1}{74}-p_2^2+\frac{1}{13}=$

If $(\alpha , \beta )$ is the image of the point $(3, -4)$ with respect to the line $4\mathrm{x}-y-1=0,$ then the value of $\beta -\alpha =\_\_\_\_\_\_\_\_\_\_$

If a point $\left(a, a\right)$ falls between the lines $|x+y|=4,$ then

If the equation of a line which divides the line segment joining the points $\left(1,0\right)$ and $\left(3,0\right)$ in the ratio $2:1$ and is also perpendicular to it, is $ax=7$, then the value of $a$ is equal to

If $m$ and $n$ are the lengths of the perpendicular from the origin to the straight lines whose equations are $x\cot \theta -y=2\cos \theta$ and $4x+3y=-\sqrt{5}\cos 2\theta$ $(\theta \in (0,\pi \left)\right),$ respectively, then the value of $m^2+5n^2$ is

If the points $\left(x,-3x\right)$ and $\left(3,4\right)$ lie on the opposite sides of the line $3x-4y=8$, then

Let $S$ be the focus of parabola $x^2+8y=0$ and $Q$ be any point on it. If $P$ divides the line segment $SQ$ in the ratio $1 : 2,$ then the locus of $P$ is

Area of the triangle with vertices $\left(-2,2\right),\left(1,5\right)$ and $\left(6,-1\right)$ is

The distance of the point $\left(3,-5\right)$ from the line $3x-4y-26=0$ is

The area of a triangle is $5$ sq units. Two of its vertices are $\left(2,1\right)$ and $\left(3,-2\right)$$.$ The third vertex lies on $y=x+3$$,$ then the coordinates of the third vertex can be

If the points $\left(2a,a\right),\left(a,2a\right)$ and $\left(a,a\right)$ enclose a triangle of area $18$ sq units, then the centroid of the triangle is equal to

The ratio, in which the line joining the points $\left(-1,1\right)$ and $\left(5,7\right)$ is divided by the line ​$x+y=1$ is